二叉树的遍历

前序、中序、后序，包括递归版本和非递归版本

完整代码

• 新建文件
• 复制粘贴
• 运行代码

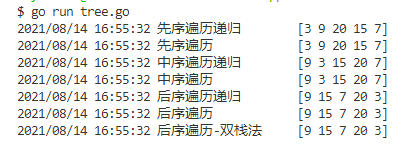
效果截图

• 测试数据
  

• 运行结果
  

代码

package main

import "log"

type Node struct {
	Val   int
	Left  *Node
	Right *Node
}

// 测试数据
// 	3
// / \
// 9  20
//  /  \
// 15   7
func main() {
	tree := Node{}
	tree.Val = 3
	tree.Left = &Node{
		Val: 9,
	}
	tree.Right = &Node{
		Val: 20,
		Left: &Node{
			Val: 15,
		},
		Right: &Node{
			Val: 7,
		},
	}
	// ------------------ end
	// 先序遍历递归
	log.Printf("%-10s\t%v", "先序遍历递归", DLRdg(&tree))
	// 先序遍历
	log.Printf("%-10s\t%v", "先序遍历", DLR(&tree))
	// 中序遍历递归
	log.Printf("%-10s\t%v", "中序遍历递归", LDRdg(&tree))
	// 中序遍历
	log.Printf("%-10s\t%v", "中序遍历", LDR(&tree))
	// 后序遍历递归
	log.Printf("%-10s\t%v", "后序遍历递归", LRDdg(&tree))
	// 后序遍历
	log.Printf("%-10s\t%v", "后序遍历", LRD(&tree))
	// 后序遍历-双栈法
	log.Printf("%-10s\t%v", "后序遍历-双栈法", LRD2(&tree))
}

// 先序遍历递归
func DLRdg(root *Node) []int {
	if root == nil {
		return []int{}
	}
	ret := make([]int, 0, 4)
	ret = append(ret, root.Val)
	left := DLRdg(root.Left)
	ret = append(ret, left...)
	right := DLRdg(root.Right)
	ret = append(ret, right...)
	return ret
}

// 先序遍历递归
func DLR(root *Node) []int {
	if root == nil {
		return []int{}
	}
	ret := make([]int, 0, 4)
	stack := make([]*Node, 0, 4)
	for root != nil || len(stack) > 0 {
		for root != nil {
			ret = append(ret, root.Val)
			stack = append(stack, root)
			root = root.Left
		}
		root = stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		root = root.Right
	}
	return ret
}

// 中序遍历递归
func LDRdg(root *Node) []int {
	if root == nil {
		return []int{}
	}
	ret := make([]int, 0, 4)
	left := LDRdg(root.Left)
	ret = append(ret, left...)
	ret = append(ret, root.Val)
	right := LDRdg(root.Right)
	ret = append(ret, right...)
	return ret
}

// 中序遍历
func LDR(root *Node) []int {
	if root == nil {
		return []int{}
	}
	ret := make([]int, 0, 4)
	stack := make([]*Node, 0, 4)
	for root != nil || len(stack) > 0 {
		for root != nil {
			stack = append(stack, root)
			root = root.Left
		}
		root = stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		ret = append(ret, root.Val)
		root = root.Right
	}
	return ret
}

// 后序遍历递归
func LRDdg(root *Node) []int {
	if root == nil {
		return []int{}
	}
	ret := make([]int, 0, 4)
	left := LRDdg(root.Left)
	ret = append(ret, left...)
	right := LRDdg(root.Right)
	ret = append(ret, right...)
	ret = append(ret, root.Val)
	return ret
}

// 后序遍历
func LRD(root *Node) []int {
	if root == nil {
		return []int{}
	}
	ret := make([]int, 0, 4)
	stack := make([]*Node, 0, 4)
	var last *Node
	for root != nil || len(stack) > 0 {
		for root != nil {
			stack = append(stack, root)
			root = root.Left
		}
		peek := stack[len(stack)-1]
		// 当前节点的右节点为空
		// 或者已经访问过了才能访问
		if peek.Right == nil || peek.Right == last {
			stack = stack[:len(stack)-1]
			ret = append(ret, peek.Val)
			last = peek
		} else {
			root = peek.Right
		}
	}
	return ret
}

// 后序遍历-双栈法
func LRD2(root *Node) []int {
	if root == nil {
		return []int{}
	}
	ret := make([]int, 0, 4)
	stack := make([]*Node, 0, 4)
	// 初始化放入根节点
	stack = append(stack, root)
	for len(stack) > 0 {
		root = stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		// // 巧妙的方式实现另外一个栈 v1
		// // 内存分配次数和元素移动次数增加
		// ret = append([]int{root.Val}, ret...)
		// // 巧妙的方式实现另外一个栈 v2
		// // 相对于 v1 减少内存分配次数
		ret = append(ret, root.Val)
		copy(ret[1:], ret[:len(ret)-1])
		ret[0] = root.Val
		if root.Left != nil {
			stack = append(stack, root.Left)
		}
		if root.Right != nil {
			stack = append(stack, root.Right)
		}
	}
	return ret
}